3.8.1 Il principio di sovrapposizione per circuiti lineari
Questo principio si applica esclusivamente a circuiti lineari, giacché discende dalla proprietà di linearità del circuito. Ricordiamo che la proprietà di linearità prevede che:
 |
f(x1 + x2) = f(x1) + f(x2) |
| f(ax) = af(x) |
Quello che questo principio afferma è che in un circuito tempo-invariante contenente sorgenti indipendenti, l'effetto ottenuto su un qualsiasi elemento passivo del circuito può essere ottenuto come sovrapposizione algebrica degli effetti di ciascuna sorgente agente da sola con tutte le altre sorgenti sostituite dalla loro resistenza interna. La risposta al tempo t dipende solo dal valore dei generatori indipendenti allo stesso tempo t, in quanto i circuiti ad elementi resistivi non hanno "memoria".
Nel caso di sorgenti ideali, la resistenza di un generatore di tensione è zero (corto circuito), mentre quella di un generatore di corrente è infinita (circuito aperto). Il principio può essere enunciato come segue:
In un circuito lineare contenente N generatori, ogni tensione e corrente di ramo è la somma, rispettivamente, di N tensioni e di N correnti ciascuna delle quali può essere calcolata mandando a zero tutti i generatori eccetto uno, e risolvendo il circuito contenente il singolo generatore.
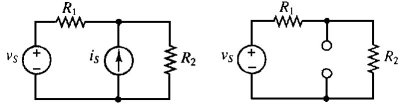
Un'illustrazione elementare del concetto può essere ottenuta facilmente considerando semplicemente un circuito con due generatori collegati in serie, come mostrato in figura 3.26:

Figura 3.26
Analizziamo ora più in dettaglio il circuito di figura 3.26. La corrente i che passa nel circuito a sinistra della figura può essere espressa così:
i = (vB1 + vB2) / R = iB1 + iB2 (F2.27)
La figura 3.26 mostra anche che il circuito è equivalente alla combinazione degli effetti di due subcircuiti, ciascuno contenente un singolo generatore. In ciascuno dei due subcircuiti, il generatore di tensione è stato sostituito con un corto circuito.
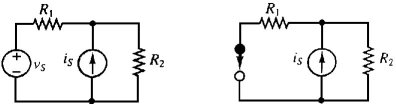
Ciò è consistente, giacché un corto circuito, per definizione, "vedrà" sempre una tensione nulla ai sui capi, e perciò questa procedura è equivalente a mandare a zero l'output di uno dei due generatori di tensione (figura 3.27a).
Per porre un generatore di tensione pari a zero, lo sostituiamo con un corto circuito.
Un semplice circuito Lo stesso circuito con vS = 0
Figura 3.27a
Se, d'altra parte, si desidera azzerare gli effetti di un generatore di corrente, si deve sostituire un circuito aperto al generatore di corrente, dal momento che un circuito aperto, per definizione, è un elemento (del circuito) attraverso cui non può passare corrente (e che perciò genererà una corrente nulla; figura 3.27b).
Per porre a zero un generatore di corrente, lo sostituiamo con un circuito aperto.
Un semplice circuito Lo stesso circuito con iS = 0
Figura 3.27b
Il principio di sovrapposizione può essere facilmente applicato a circuiti contenenti più generatori, e talvolta è un'efficace soluzione tecnica. Più spesso, tuttavia, altri metodi danno una soluzione in maniera più efficiente e meno "pesante" dal punto di vista computazionale. Per rendersene conto, si invita per esercizio a provare a risolvere gli esempi 3.5.2 e 3.5.3 con questo metodo.
3.8.2 Esempio
Useremo ora il circuito di figura 3.27 ed il principio di sovrapposizione per determinare la corrente attraverso il resistore R2. Si assuma che: vS = 6 V, iS = 0.5 A, R1 = 50 Ω, R2 = 100 Ω.
La corrente attraverso il resistore R2 nel circuito di figura 3.27 è dovuta alla sovrapposizione degli effetti dei due generatori. Siano ii2 e iv2 le correnti che attraversano il resistore R2 dovute, rispettivamente, al generatore di corrente ed a quello di tensione. Allora, in base alla regola di partizione delle correnti:
ii2 = 0.5 × R1 / (R1 + R2) = 1/6 A
e per la regola di partizione delle tensioni e per la legge di Ohm:
iv2 = 6 × R2 / (R1 + R2) = 1/25 A
Infine, per il principio di sovrapposizione, la corrente i2 che passa per il resistore R2 è data da:
i2 = ii2 + iv2 = 1/6 + 1/25 = 0.207 A
Si può per esercizio verificare che questa soluzione è corretta usando l'analisi per nodi o per maglie.




