3.9.1 Reti ad ingresso singolo

Ricordando la discussione fatta nel Capitolo 2 relativamente ai generatori ideali (Cfr. Lezione 2.03), concettualmente il flusso di energia da un generatore ad un carico può essere descritto in una forma molto generale, mediante la connessione di due "scatole" chiamate generatore e carico (figura 3.28a).

Nella stessa figura 2.8 erano mostrate altre due descrizioni dello stesso concetto: una simbolica, mostrante un generatore di tensione ed un resistore ideale, ed una fisica, in cui il carico era costituito da un faro ed il generatore da una batteria d'automobile.

Qualunque sia la forma grafica prescelta per la rappresentazione del sistema generatore-carico, ciascun blocco (generatore o carico) può essere visto come un dispositivo a due terminali, descritto da una sua caratteristica i-v.

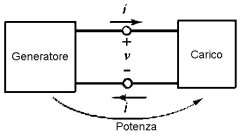Figura 3.28a

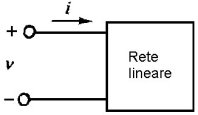Figura 3.28b

Questa rappresentazione generale del circuito è mostrata in figura 3.28b. Questa rappresentazione è chiamata rete ad ingresso singolo ed è particolarmente utile per introdurre la nozione di circuito equivalente.
   In generale, la rete che fornisce la corrente (source) oltre a contenere (ovviamente) generatori (di cui almeno uno deve essere indipendente), potrà contenere anche altri elementi circuitali (ad esempio, resistori); analogamente per la rete che assorbe la corrente (load). Lo vedremo.
Si noti che la rete di figura 3.28 è completamente descritta dalla sua caratteristica i-v; questo fatto è meglio illustrato dal seguente esempio.

3.9.2 Esempio

Consideriamo il circuito mostrato in figura 3.29.

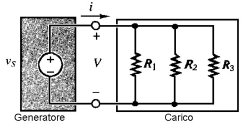
Figura 3.29

Se, ad esempio, volessimo determinare la richiesta di corrente fatta dalla rete resistiva a scapito del generatore di tensione, dovremmo calcolare la corrente i fornita dal generatore in base alla seguente espressione:

i = v_s / (1 / (1/R₁ + 1/R₂ + 1/R₃))

Dovrebbe risultare chiaro per quel che riguarda il generatore è irrilevante che il carico sia costituito da tre resistori in parallelo o da un singolo resistore equivalente di resistenza pari a:

R_EQ = 1 / (1/R₁ + 1/R₂ + 1/R₃)

In ogni caso, noi possiamo rappresentare il carico per mezzo di un singolo resistore di resistenza equivalente R_EQ, come mostrato in figura 3.30.

   
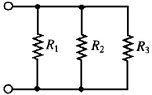
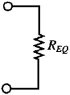
Figura 3.30 Circuito di carico ed il suo equivalente

   Similmente, se il generatore di tensione consiste di una batteria da 6 V, per quel che riguarda il carico è irrilevante che il circuito generatore sia costituito da una singola batteria da 6 V o da quattro batterie in serie da 1.5 V ciascuna. Questo porta a delle conseguenze importanti che discuteremo nel prossimo paragrafo.

3.9.3 Circuiti equivalenti di Thévenin e di Norton

Discuteremo ora l'importantissimo concetto di circuito equivalente. In base a quanto detto fin qui, mostreremo che è sempre possibile vedere circuiti anche complicati in termini di circuiti equivalenti molto più semplici, costituiti da un generatore ed un carico, e che le trasformazioni che portano al circuito equivalente sono gestibili facilmente con un po' di pratica. Nello studiare l'analisi per nodi e l'analisi per maglie, si sarà probabilmente notato che c'è una certa corrispondenza (dualità) tra i generatori di corrente ed i generatori di tensione, da un lato, ed i circuiti in serie ed in parallelo, dall'altro.

Questa dualità compare di nuovo molto chiaramente nell'analisi dei circuiti equivalenti: mostreremo brevemente che i circuiti equivalenti ricadono in una delle due classi, coinvolgendo o i generatori di tensione o quelli di corrente e (rispettivamente) o resistori in serie o resistori in parallelo, riflettendo tale principio di dualità.

La discussione sui circuiti equivalenti inizia con gli enunciati di due teoremi molto importanti, sintetizzati nelle figure 3.31 e 3.32.

Teorema di Thévenin: Nei confronti del carico, ogni rete costituita da generatori ideali di corrente e/o tensione, e da resistori lineari, può essere rappresentata come un circuito equivalente che consiste di un generatore ideale di tensione, v_T, in serie con una resistenza equivalente, R_T.

Figura 3.31 Illustrazione del teorema di Thévenin

Teorema di Norton: Nei confronti del carico, ogni rete costituita da generatori ideali di corrente e/o tensione, e da resistori lineari, può essere rappresentata come un circuito equivalente che consiste in un generatore ideale di corrente, i_N, in parallelo con una resistenza equivalente, R_N.

Figura 3.32 Illustrazione del teorema di Norton

La prima domanda che sorge spontanea è: come si calcolano correnti, tensioni e resistenze equivalenti?

Nel prosieguo del corso illustreremo come si procede nei calcoli, soprattutto tramite esempi. Tuttavia, il solo modo per acquisire dimestichezza con questi metodi è fare pazientemente numerosi esercizi.